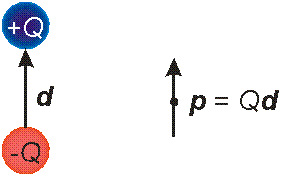
ELEKTRIČNI DIPOL

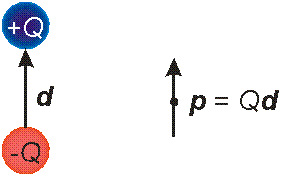
Električni dipolni moment predstavimo kot par nabojev, enega pozitivnega in enega negativnega, ki sta fiksno povezana z »distančnikom«, ki ga opišemo z vektorjem d. Kljub neki končni dimenziji smatramo, da je dipol tako majhnih dimenzij, da ga lahko »postavimo« v določeno točko. Opozoriti velja, da je električni dipolni moement definiran kot produkt naboja in vektorja d: p = Qd, pri čemer je vektor d usmerjen od negativnega naboja v smeri pozitivnega (v nasprotni smeri kot bi bilo polje med pozitivnim in negativnim nabojem). Razlog je v tem, da je definiran tako, da se v primeru možnosti prostega vrtejna usmeri v smer zunanjega polja.

Primeri grafičnih prikazov potenciala in polja v okolici električnega dipola

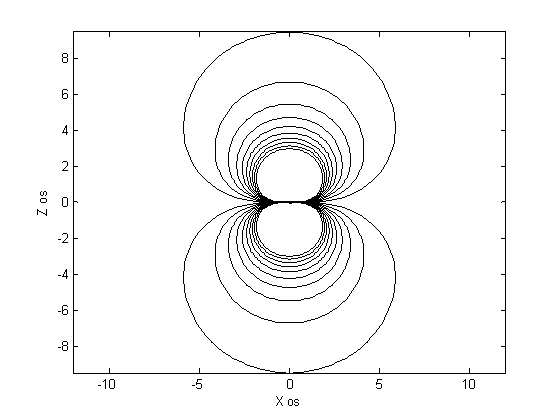
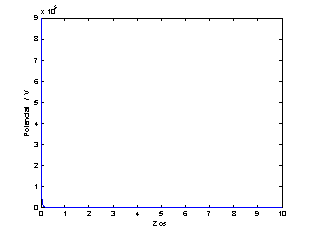
 Vzemimo električni dipol, ki se nahaja v koordinatnem izhodišču. Izrišimo ekvipotencialne ravnine za dipolni moment p = 10^-8 Cm, ki je usmerjen v smeri osi Z. Poleg tega izrišimo potek potenciala vzdolž Z osi.

1.      NAČIN:

Vzemimo električni dipol, ki se nahaja v koordinatnem izhodišču. Izrišimo ekvipotencialne ravnine za dipolni moment p = 10^-8 Cm, ki je usmerjen v smeri osi Z. Poleg tega izrišimo potek potenciala vzdolž Z osi.

Izračun: Uporabimo enačbo

 ,

kjer za določene napetosti (od 0 do 10 V ) in vrednosti theta od 0 do pi določimo vrednosti radija. Te pretvorimo v vrednosti na X osi in Z osi.

% dipol.m

% izris ekvipotencialnih ravnin v okolici dipola

for Veq=0:1:10

p=1e-8;

eps0=8.854e-12;

k=p/(4*pi*eps0*Veq);

theta=0:pi/100:pi;

r=sqrt(k.*cos(theta))

x=r.*sin(theta);

z=r.*cos(theta);

plot(x,z,-x,z,-x,-z,x,-z)

set(findobj('Type','line'),'Color','k')

xlabel('X os');

ylabel('Z os')

axis equal

hold on

end

figure;

k=p/(4*pi*eps0);

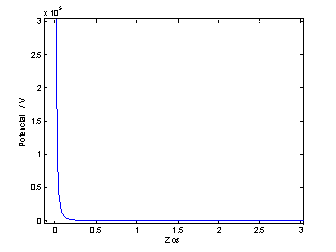
r=0:0.01:10;

V=k./r.^2

plot(r,V)

xlabel('Z os');

ylabel('Potencial   / V')

DRUGI NAČIN IZRAČUNA IN IZRISA EKVIPOTENCIALNIH RAVNIN IN IZRAČUN ELEKTRIČNE POLJSKE JAKOSTI (dipol_potencial1.m)

Za izračun polja uporabimo izraze:

.

Opomba: Polje v okolici dipola zelo hitro upada. Zato za izris z vektorji normiramo vrednosti. Vektorji torej kažejo le smer ne pa tudi velikosti.

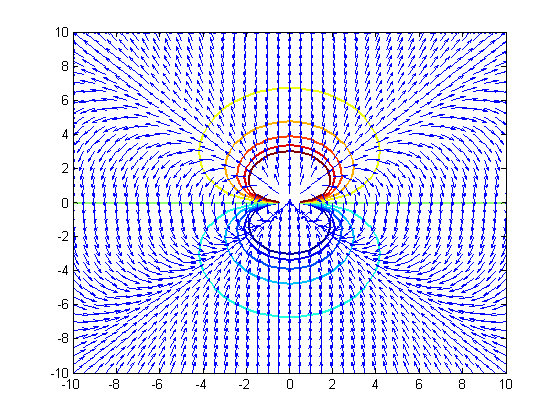
Matlab: Z Matlab funkcijo meshgrid določimo točke, v katerih izračunamo potenciale. Za izris ekvipotencialk uporabimo ukaz contour, za izris normiranih vektorjev polja pa quiver.

% dipol_potencial1.m

p=1e-8;

eps0=8.854e-12;

k=p/(2*pi*eps0);

[x,z] = meshgrid(-10:.5:10);

r=sqrt(x.^2+z.^2);

theta=acos(z./r);

V=k*cos(theta)./r.^2/2;

veq=[-10 -8 -6 -4 -2 0 2 4 6 8 10];

contour(x,z,V,veq, 'LineWidth',2);

%break

hold on

Er=k*cos(theta)./(r.^3);

Eth=k*sin(theta)./(r.^3)/2;

Ex=Er.*sin(theta)-Eth.*cos(theta);

Ex=sign(x).*Ex;

Ez=Er.*cos(theta)-Eth.*sin(theta);

absE=sqrt(Ex.^2+Ez.^2);

quiver(x,z,Ex./absE,Ez./absE,'AutoScaleFactor',1)

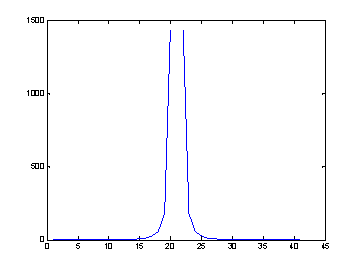
Polje v smeri osi Z se spreminja (manjša) s tretjo potenco, kar lahko prikažemo tako,  da uporabimo izraz plot(Ez(:,21)), ki nam da vrednosti vzdolž Z osi pri x=0.

TRETJI NAČIN IZRAČUNA POLJA: IZ GRADIENTA POTENCIALA

Matlab: Z Matlab funkcijo gradient numerično odvajamo izračunano funkcijo potenciala na mreži točk, ki smo jih določili s funkcijo meshgrid. Za izris ekvipotencialk uporabimo ukaz contour, za izris normiranih vektorjev polja pa quiver.

% dipol_potencial2.m

p=1e-8;

eps0=8.854e-12;

k=p/(2*pi*eps0);

[x,z] = meshgrid(-10:.5:10);

r=sqrt(x.^2+z.^2);

theta=acos(z./r);

V=k*cos(theta)./r.^2/2;

veq=[-10 -8 -6 -4 -2 0 2 4 6 8 10];

contour(x,z,V,veq);

%[C,h]=contour(x,z,V,veq);

% clabel(C,h)

hold on

[EX,EZ] = gradient(-V,.2,.2);

Enorm=sqrt(EX.^2+EZ.^2);

quiver(x,z,(EX./Enorm),(EZ./Enorm),1);

%colormap hsv

grid off

hold off

xlabel('X os');

ylabel('Z os')