Falling_Ball_efield3

Contents

Observations

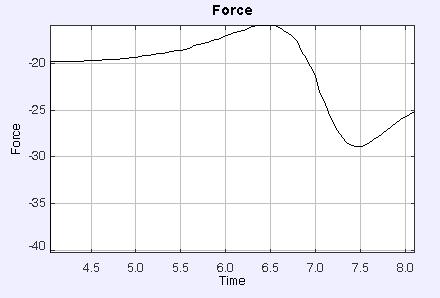
1. The charge of the ball is small and of equal sign as the charge of the ring

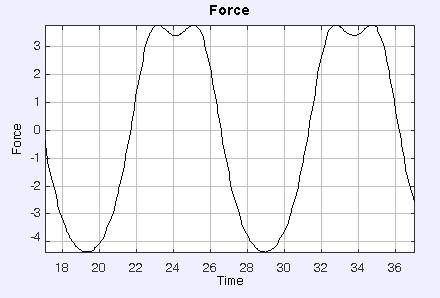
The repulsive electric field is not strong enough to repel the ball from the ring. The ball falls through the ring and dissapears.Observe plot of the force. Gravitational force is always equal (m*g) but up to the center of the ring the total force is reduced due to repulsive action of the ring.After that the repulsive force between the charges adds to the gravitational force and increases the velocity of the falling ball. At larger distances from the ring the electric force is reduced.

2. The charge of the ring is large and of equal sign as the charge of the ball.

The electrical force between the ring and the ball is strong and if it exceeds the gravitational force than the ball moves up and bounces from the top.This repeats forever in case no energy is lost in bouncing or in air (friction).

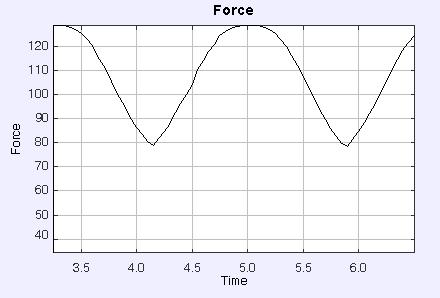
3. Oscilation of a charged ball through the ring

If the kinetic energy of the ball is not larger than the electric potential energy, the ball is trapped by the ring and the charged ball oscillates inside the ring.

First the attractive force pushes the oppositely charged ball upwards and shoots it through the ring. After that both gravitational and electrical force point towards bottom.The electrical force is pointing upwards when the ball is below the ring and downwards when it is above the ring.

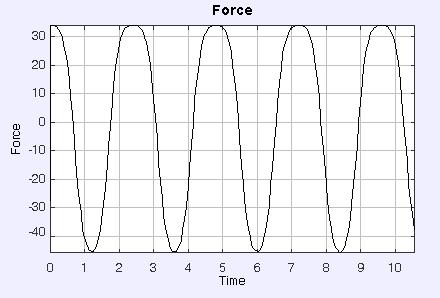
The shape of the force plot is not completely sinusoidal.Try to find out why?

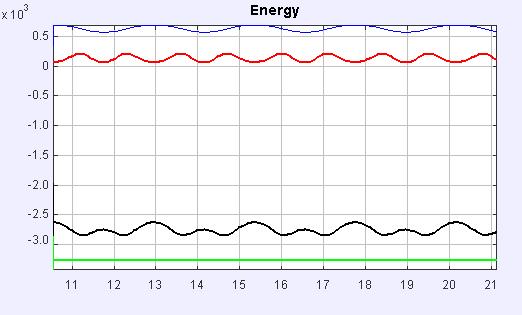
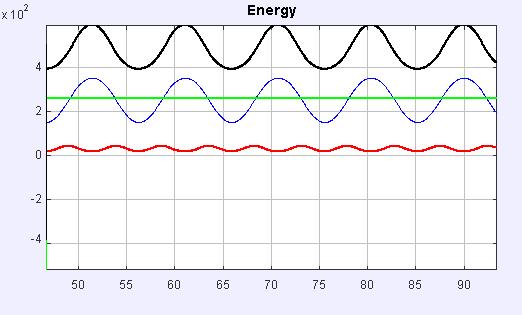
Electrical potential energy is negative since the charge of the ring is negative. Gravitational potential energy oscialates in a similar manner as the force - with the distance from the ring. On the other hand, the kinetic energy oscilates with a double frequency. It is zero at the top and bottom positions (velocity is zero) and maximal at the middle of the ring.

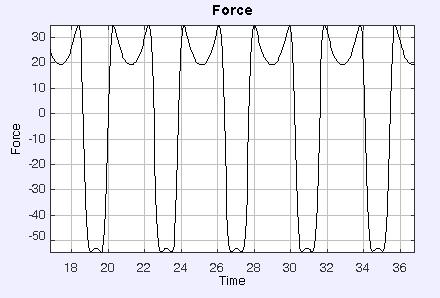
Interesting enough the plot below shows a little bit different time development of the force. It shows two maxima (and also possibly minima). These two maxima are observeed when the ball supeceeds the point of maximal electric field. At the bottom and at the top. The top maxima are obtained when the ball is near the lowest point.

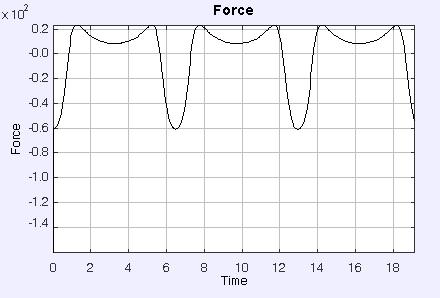
Again another force/time plot is observed when one increases the mass of the particle. This increases the gravitational force but not the electrical one. See figure below.

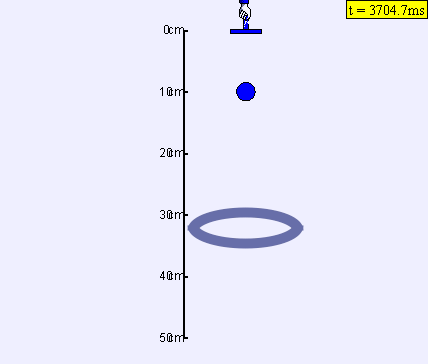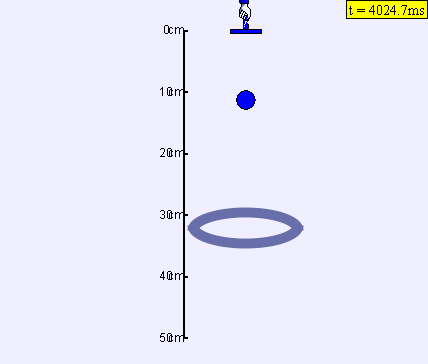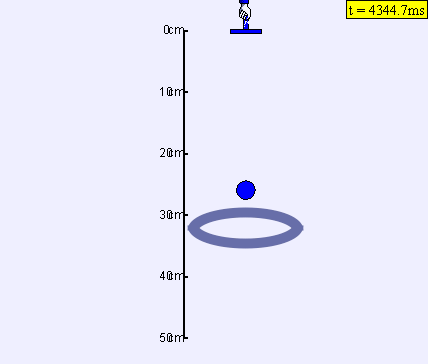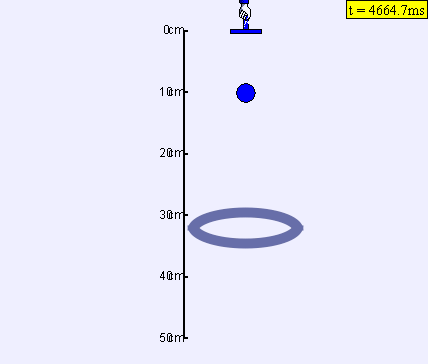
3. Oscilation of a charged ball above the ring

In case we position the ring closer to the equally charged ring the kinetinc energy could be lower than the electrical potential energy. In such case a particle will oscillate above the ring.

Why should you try it? > Because it is fun. Besides - you learn. 

Falling Charged Ball through a charged Ring

The charged ball is released and falls due to a gravitational force. The ball and the ring can be charged with a positive (colored in blue) or  a negative charge (colored in red). This adds an additional repulsive or attractive force between the fixed ring and the ball. The ball can be moved to a suitable height by dragging it with a mouse. The charged ring is located directly below the ball. Besides, the mass of the ball can be modified.

One can observe several scenarios:

1. The ball is heavy and starts far away from the charged ring. The ring and the ball can be equally or oppositely charged.

2. The ball is light and starts far away from the ring. The ring and the ball can be equally or oppositely charged.

3. Modify the magnitude and sign of charge on the ball and the ring and observe the effects.

4. Position the ball charged below the ring. Set the charge of the ring and the ball so that they are attracted. Observe the resulting movement of the ball.

4. In a certain case it is possible to trap the ball by suitably charging the ring and with suitable initial conditions (height and mass of a ball). Find these situations.

Suggestions

• Find equations describing the force between the point charge located above the charged ring. Look at the point of the largest force and how much force there is in the middle of the ring.
• Increasing the mass of a ball can result in the ball falling through the ring. Why?
• Put a ball below the ring. The ball and the ring should be oppositely charged. The force is strong enough that the electrical force is larger than the force of gravity. Is is possible that by starting the simulation the ball will move through the ring and to a  larger distance between the ball and the ring than it was in the beginning? Will the ball find a stable (stationary) position.

Credits

The Falling Ball in Electric field was motivated by the simulation example "The Falling Cup with Ball" that was created by Wolfgang Christian. Thanks to Francisco Esquembre for developing the EJS software. Author of a modified code: Dejan Križaj. All members of the Colos group (Conceptual learning of Science).

Reuse the model

You can examine and modify the physical model for this simulation if you have Ejs installed by right-clicking within the wave function plot and selecting "Open Ejs Model" from the pop-up menu.  As a part of the code was reused it was not completely removed from the code. This makes some variables and programming in the code unnecessary.

Information about EJS is available at: <http://www.um.es/fem/Ejs/> and in the OSP comPADRE collection <http://www.compadre.org/OSP/>.