REŠEVANJE SISTEMA ENAČB S PROGRAMOM MATLAB
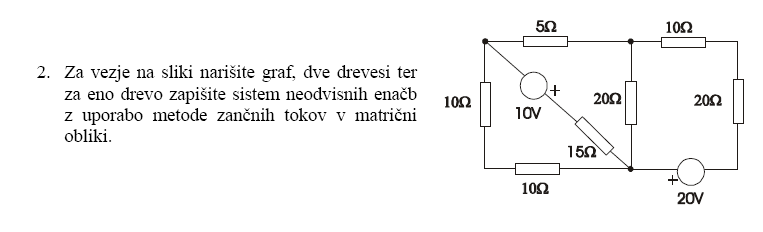
Kot primer vzemimo izpitno nalogo 31.5.2005:

Rešitev:
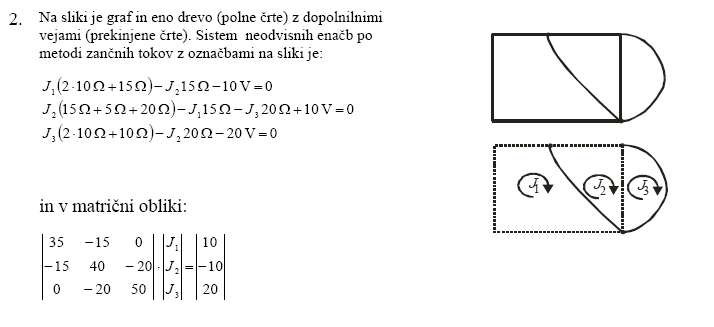
Rešimo sedaj sistem enačb, ki je zapisan v matrični obliki. V Matlabu to lahko naredimo na več načinov:
1. Matrično enačbo zapišemo v obliki A.x=b, kjer je A matrika, ki jo v Matlabu zapišemo v naslednji obliki:
A=[35,-15,0;-15,40,-20;0,-20,50]
Če to zapišemo v ukazni vrstici Matlaba, je rezultat ob pritisku tipke Enter:
A =
35 -15 0
-15 40 -20
0 -20 50
Zapišemo še vektor b (znane vrednosti na desni strani enačbe):
b=[10;-10;20]
Matlab "odgovori":
b =
10
-10
20
Opozarjam na pomen uporabe podpičja pri zapisu vektorja b. Za pravilno uporabo enačb potrebujemo vektor v obliki stolpca in ne vrstice.
Rešitev dobimo z uporabo ukaza
x=A\b
in dobimo
x =
0.3240
0.0894
0.4358
Kaj to pomeni? x(1)=J1=0.324 A, x(2)=J2=0,0894 A in x(3)=0,4385 A.
2. Podoben način je ta, da izračunamo inverzno matriko matrike A in jo pomnožimo z vektorjem b. To naredimo s sledečim ukazom:
x=inv(A)*b
Rezultat je
x =
0.3240
0.0894
0.4358
torej enako kot v prejšnjem primeru.
3. Sistem enačb rešimo z determinantami. Rešitev x(1) je enaka kvocientu poddeterminante A1 in determinante matrike A. Poddeterminanto A1 dobimo tako, da prvi stolpec matrike A zamenjamo z vektorjem b. Determinante izračunamo z uporabo ukaza det:
det(A)
ans =
44750
Rezultat je 44750. Sedaj tvorimo matriko A1
A1=[10,-15,0;-10,40,-20;20,-20,50]
dobimo
A1 =
10 -15 0
-10 40 -20
20 -20 50
det(A1)
Rezultat je 14500. Sedaj naredimo le še kvocient:
x1=det(A1)/det(A)
Rezultat je 0,3240, enak kot za x(1) v prvem primeru reševanja.
Drugi dve rešitvi dobimo kot x1=det(A2)/det(A) in x3=det(A3)/det(A).
Kako dobimo A2 in A3? A2 dobimo tako, da v matriki A zamenjamo drugi stolpec z vektorjem b. Itd.
Sestavil: D. Križaj