Magnetno polje dveh vodnikov, če teče tok v nasprotno smer. |
Magnetno polje dveh vodnikov, če teče tok v isto smer. |
Primeri nalog iz Osnov elektrotehnike 2 rešeni s programom MATLAB
1. Primer: Gostota magnetnega pretoka vzdolž osi tuljavice
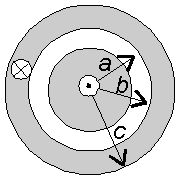
2. Primer: Gostota magnetnega pretoka v koaksialnemu kablu
Za ogled ostalih primerov shranite datoteko vaje.zip, jo razpakirajte ter poženite datoteko vaje.m v okolju programa Matlab. Primere je izdelal Andrej Krenker, študent FE.
V sklopu te aplikacije je prikazanih 5 primerov:
- Gibanje elektrona v magnetnem polju: (vaja1r.m)
Elektron leti z določeno hitrostjo pod kotom na z os. Ko prileti skozi koordinatno izhodišče vklopimo magnetno polje, ki kaže v smeri osi z in opazujemo njegovo trajektorijo leta.
- Gibanje elektrona v električnem in magnetnem polju: (vaja2r.m)
Vzdolž z osi je homogeno magnetno polje, vzdolž y osi pa homogeno električno polje. Elektron ima v času t=0 hitrost v smeri osi z. Opazujemo trajektorijo leta.
- Magnetno polje v osi tuljave: (vaja3r.m)
Ta primer je prikazan z manjšimi spremembami v nadaljevanju
- Jakost magnetnega polja v koaksialnem kablu (vaja4r.m)
Ta primer je prikazan z manjšimi spremembami v nadaljevanju
- Magnetno polje v okolici dveh premih vodnikov (vaja5r.m)
Prikazuje magnetno polje v okolici dveh premih vodnikov (dvovoda), pri čemer lahko teče tok v isto ali nasprotno smer. Vsebuje 2D prikaze z vektorji in gostotnicami.
Magnetno polje dveh vodnikov, če teče tok v nasprotno smer. |
Magnetno polje dveh vodnikov, če teče tok v isto smer. |
| Izhajamo iz znanega
izraza za magnetno polje v osi tokovne zanke in s seštevanjem (integracijo) delnih
prispevkov ovojev izpeljemo izraz (glej auditorne vaje in predavanja):
|
|
Vhodni podatki:
|
|
| function vaja3b |
| % IZRACUN POLJA B V SREDINI TULJAVE |
| %Vnos podatkov |
| r = input('Polmer tuljave (v [m] ali R=0.02m): '); |
| if isempty(r); r=0.02 |
| end; |
| l=input('Dolzina tuljave (v [m] ali L=0.1): '); |
| if isempty(l); l=0.1 |
| end; |
| n=input('Stevilo ovojev ali N=1000:'); |
| if isempty(n); n=1000 |
| end; |
| i=input('Tok skozi en ovoj ali I=1A (v [A]): '); |
| if isempty(i); i=1 |
| end; |
| % Definiram koordinato Z |
| z=[-l*1.5:.01*l:l*1.5]; |
| % Izracun polja |
| b=2*pi*n*i*10^(-7)*((z+l/2)./sqrt(r^2+(l/2+z).^2)+(l/2-z)./sqrt(r^2+(l/2-z).^2))/l; |
| % Prikaz rezultatov |
| figure; |
| axes('Units','normalized') |
| plot(z,b,'linewidth',4) |
| xlabel('x / m'); |
| ylabel('B / T'); |
| Izračunamo gostoto pretoka znotraj
koaksialnega kabla z uporabo Ampereovega zakona. Le-tega moramo uporabiti posebaj za
notranjost žile, v izolatorju in v plašču. Dobimo:
|
|
Vhodni podatki:
|
 |
function vaja4c % Polje B v koaksialnem kablu % v primeru, da ima kabel magnetne lastnosti, moramo polje v prevodniku pomnoziti % z relativno permeabilnostjo mr m0=4*pi*1e-7; mr=1; % Preberem globalne spremenljivke in jih iz nizov pretvorim v stevila a = input('Polmer notranje zile v [m]: '); if isempty(a); a=0.01 end; b=input('Polmer zunanje plasti izolatorja v [m]: '); if isempty(b); b=0.02 end; c=input('Polmer zunanje plasti kabla v [m]:: '); if isempty(c); c=0.03 end; i=input('Tok v notranji zili v [A]: '); if isempty(i); i=1 end; % Definiram podrocje izrisa r1=[0:.01*a:a]; r2=[a:.01*b:b]; r3=[b:.01*c:c]; %IZRACUN % Notranja zila B1=mr*m0*i*r1/(2*pi*a^2); % Izolacija B2=m0*i./(2*pi*r2); % Zunanja zila B3=mr*m0*i*(c^2-r3.^2)./(2*pi*r3*(c^2-b^2)); % Predstavitev rezultatov figure; axes('Units','normalized'); plot([r1 r2 r3],[B1 B2 B3]) xlabel('r / m'); ylabel('B / T');