OSNOVE ELEKTROTEHNIKE I - ELEKTROSTATIKA
s programom MATLAB
(ver. 2.1)
Dejan Križaj
Fakulteta za elektrotehniko, Univerza v Ljubljani, Tržaška 25, 1000 Ljubljana
Email: dejan.krizaj@fe.uni-lj.si
http://lbm.fe.uni-lj.si/dejan/OE/MATLAB/Mlab_oe1.html
POGLAVJA:
1. Elektrina (naboj), sila med elektrinami
2. Sila na tockaste elektrine - Coulombov zakon
6. Energija elektrostaticnega polja
Literatura
Pri študiju elektrotehnike (in ostalih ved naravoslovja) se pogosto srečamo s problemom računanja in vizualizacije rezultatov. Pri tem so nam lahko v veliko pomoč različni programski paketi, med katerimi se v tehniških vedah zelo pogosto uporablja program Matlab. Matlab je posebno primeren za reševanje matričnih zapisov enačb, ki pri elektrotehniki zelo pogosto nastopajo. Uvede nas tudi v način preprostega programiranja, ki nam olajša prehod na programiranje v bolj zahtevnih programskih jezikih.
Program Matlab se vedno bolj pogosto uporablja tudi v višjih letnikih študija na Fakulteti za elektrotehniko, zato je zgodnje seznanjanje s programom koristno tudi za nadaljnji študij.
V tekstu so opisani primeri
nalog, ki predstavljajo
Elektrina je kvantizirana. Osnovna elektrina (naboj) elektrona je q0=-1,609.10-19 As. Enota za elektrino je [A.s]=[C].
Sila med elektrinama je proporcionalna produktu velikosti elektrin in nasprotno proporocionalna kvadratu razdalje med elektrinama.
Konstanta proporcionalnosti je 
.
Naloga 0.1: Jedro atoma železa ima radij 4.10-15 m in vsebuje 26 protonov. Kolikšna je elektrostaticna sila med dvema protonoma, ki sta razmaknjena za 4.10-15 m?
% Izracun sile med elektrinama. Znak za komentar je %
q0=1.609e-19
% ce stavka ne zakljucimo s podpicjem (;) se izpise sproten rezultat
k=9e9;
r=4e-15;
F=k*q0^2/r^2; %izracun
strF=num2str(F); %pretvorba v string
disp(['Sila je ' strF ' N']); %izpis
Sila je 14.5625 N
Vprašanja:
- Ali je ta sila odbojna ali privlacna?
- Kolikšna je elektrostatična sila v primerjavi z gravitacijsko silo med protonoma? (g=6,67.10-11 Nm2/kg2, mp=1,67.10-27 kg)
- (Zakaj se jedro železa ne razleti?)
Naloga 0.2: Kolikšna je elektrostatična sila med natrijevim ionom (Na+ elektrina +q0) in klorovim ionom (Cl-, elektrina -q0) v kristalu soli, če sta iona razmaknjena za 2.82.10-10 m?
Naloga 0.3: Dva identična iona, razmaknjena za 5.10-10 m, se odbijata s silo 3,7.10-9 N. Kolikšna je elektrina vsakega od ionov? Koliko elektronov "manjka" (je preveč), da bi bila iona nevtralna?
2. Sila na točkaste elektrine- Coulombov zakon
Sila med elektrinama je usmerjena vzdol premice na kateri se nahajata elektrini. Spreminja se inverzno proporcionalno s kvadratom razdalje med elektrinama in je proporcionalna velikosti obeh elektrin: Sila na elektrino Q2 je:
kjer je 
enotin vektor v smeri od
elektrine Q1 do Q2. Če je elektrin več, je sila
na elektrino (vektorska) vsota prispevkov posameznih
elektrin (superpozicija!).
Naloga 1.1: Elektrina Q1=2 m C se nahaja v središču koordinatnega sistema P1(0,0,0)m. S kolikšno silo deluje na elektrino Q2=-3 m C, ki se nahaja v točki P2(1,3,2) cm?
Namen: Seznanitev z vektorskim računom ter izračun sile na elektrino v poljubni točki.
MLAB: Vrstični vektor zapišemo tako, da nizamo komponente vektorja v oglatem oklepaju (r1=[0, 0, 0]). Absolutno vrednost vektorja dobimo tako, da skalarno pomnožimo vektor s samim seboj (Abs_r21=sqrt(r21*r21');). Potrebno je biti pozoren na to, da je v MATLABU potrebno množiti vektor s transponiranim vektorjem, ki ga označuje zgornji apostrof (').
Q2=-3e-6 % če vrstiče ne zaključimo z znakom";", se izpiše rezultat
e0=8.854e-12; % dielektričnost vakuuma
k=1/(4*pi*e0);
-3.0000e-006 % izpis rezultata
r1=[0, 0, 0]; %vrstični vektor
r2=[1,3,2]*1e-2;
r21=r2-r1; % vektor, ki kaže od vektorja r1 proti vektorju r2 oz. iz izhodišča v točko P2
Abs_r21=sqrt(r21*r21'); % absolutna vrednost vektorja r21 dobimo z množenjem vektorja r21 s transponiranim vektorjem r21'
er21=r21/Abs_r21 % normalni vektorj v smeri r21
0.2673 0.8018 0.5345
F21=k*Q1*Q2*er21/Abs_r21^2 % sila na elektrino Q2
Abs_F21=sqrt(F21*F21')
38.5189
-10.2946 -30.8838 -20.5892
Vprašanja:
a) V katero smer kaže sila na elektrino?
b) V kateri smeri je največja sila?
c) Koliko je absolutna vrednost sile (enote!)?
d) Koliko prostih elektronov vsebujeta Q1 in O2?
e) Kolišna je sila v smeri vektorja d=(1,2,0)? (Uporabi skalanrni produkt vektorja z enotinim vektorjem v smeri vektorja d!)
Naloga 1.2: Poleg dveh elektrin iz naloge 1 imamo še elektrino Q3=1 m C na mestu P3(-1,0,2)cm. Vsota vseh treh elektrin je enaka 0, kar zaključuje sistem elektrin. Ponovno izračunajte silo na elektrino Q2!
Namen: Uporaba superpozicije za izračun sile v sistemu več točkastih elektrin.
MLAB: Ker smo silo Q1 na Q2 že izračunali, izračunamo le še prispevek elektrine Q3 in prispevka seštejemo:
r3=[-1,0,2]*1e-2;
r23=r2-r3
Abs_r23=sqrt(r23*r23');
er23=r23/Abs_r23;
F23=k*Q1*Q2*er23/Abs_r23^2 % sila na elektrino Q2
Abs_F23=sqrt(F23*F23')
F2=F21+F23 % celotna sila na elektrino Q2
r23 =
0.0200 0.0300 0
F23 =
-23.0100 -34.5150 0
Abs_F23 =
41.4819
F2 =
-33.3046 -65.3988 -20.5892
Vprašanja:
- Katera sila je večja, F21 ali F23 in zakaj?
- * Kako bi izračunali silo na elektrino v primeru 10-ih elektrin?
- ** Kam bi morali postaviti elektrino Q3, da bi bila sila nanjo enaka nič?
Naloga 1.3 Določite silo na elektrino Q1 iz naloge 1.1!
Naloga 1.4 Določite silo na elektrino Q1 iz naloge 1.2!
Naloga 1.5 Elektrinam v nalogi 1.2 poljubno spreminjamo predznak. Kdaj bo sila na elektrino Q3 največja in kdaj najmanjša in koliko bo?
Naloga 1.6P: Uporaba elektrostatične sile med delci: Primer izračuna elektrostatične sile ne cezijev ion v molekuli cezijevega klorida!
V molekuli cezijevega klorida (CsCl) so cezijevi ioni (Cs+) nameščeni v vogalih kocke, ki ima dolžino stranice a=0,4 nm, klorov ion (Cl-) pa je v centru kocke. Kolikšna je sila na klorov ion? Ce manjka en cezijev ion, recemo, da ima kristal defekt. Kolikšna je sila na klorov ion v tem primeru?
Električno poljsko jakost definiramo kot silo na enoto poskusne elektrine q. V tem smislu lahko izračunamo električno poljsko jakost povsod v prostoru, kjer se nahajajo elektrine. V prostoru N točkastih elektrin je električna poljska jakost na mestu določenim z vektorjem rk vsota prispevkov vseh elektrin:
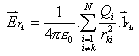
Naloga 2.1 V prostoru imamo elektrini Q1=2 pC v točki P1(1,1,1)mm in Q2=-2 pC v točki P2(-2,-1,3) cm. Koliko je električna poljska jakost v središču koordinatnega sistema?
Namen: Izračun električne pojske jakosti v poljubni točki prostora kot superpozicija prispevkov.
Q2=-2e-12;
e0=8.854e-12;
r0=[0,0,0];
r1=[1, 1, 1]*1e-2;
r2=[-2,-1,3]*1e-2;
% tvorimo vektor, ki kaže od točke P2 (vektor r2) proti točki središču k.s. (vektor r0)
r20=r0-r2;
r10=r1-r0;
Abs_r20=sqrt(r20*r20');
er20=r20/Abs_r20;
Abs_r10=sqrt(r10*r10');
er10=r10/Abs_r10;
E20=k*Q2*er20/Abs_r20^2 % polje zaradi elektrine Q2
E10=k*Q1*er10/Abs_r10^2 % polje zaradi elektrine Q1
E0=E20+E10
Abs_E0=sqrt(E0*E0')
6.8631 3.4315 -10.2946
E10 =
34.5938 34.5938 34.5938
E0 =
41.4569 38.0254 24.2992
Abs_E0 =
61.2785
Naloga 2.2: Določite električno poljsko jakost na mestu P4(1,1,1)cm za elektrine iz naloge 1.2!
Naloga 2.3: Elektrini Q1=1 m C in Q2=-3 m C sta razmaknjeni za 12 cm in se nahajata vzdolž x osi. Izrišite električno poljsko jakost vzdolž x osi!
Namen: Izračun polja za poljubno točko v prostoru. Seznanitev z zapisom vektorjev in matrik ter operacij med njimi.
MLAB: Vektor točk vzdolž x osi od –2 cm do 2 cm po koraku
0.1 zapišemo kot X=(-2:0.1:4)*1e-2; . Množenje vektorja a z
vektorjem b (a*b) je skalarni produkt. En vektor mora
biti vrstica, drugi stolpec, rezultat je skalar. Množenje
(deljenje) komponent vektorja a s komponentami vektorja b brez dodatnega seštevanja
delnih množenj (deljenj), dosežemo z operacijo (.*) ali (./). Za izris grafa si poglejte pomoč
v MLABu (help plot).
Q1=1e-6;
Q2=-3e-6;
e0=8.854e-12;
k=1/(4*pi*e0);
X=(-2:0.5:2)*1e-2; % koordinate x osi
% Q1 postavimo v koord. izhodišce, Q2 pa 2 cm stran v smeri poz. x osi
E1=k*Q1*X./abs(X).^3; % operator za deljenje vektorja je "./"
XT=2*1e-2*ones(1,length(X)); %vektor z vrednostmi pozicije lektrine Q2
Xraz=X-XT;
E2=k*Q2*Xraz./abs(Xraz).^3;
E=E1+E2;
plot(X,E1,'+-',X,E2,'*-', 'Linewidth',1.5)
xlabel('X os [cm]');
ylabel('E1, E2 [V/m]');
Vprašanja:
- Kakšna je smer polja vzdolž x osi?
- Koliko je najmanjša velikost polja med elektrinama?
- Kje je polje enako nič?
- Kakšno bi bilo polje, če bi bila tudi druga elektrina pozitivna?
- Kakšno bi bilo polje, če bi bili obe elektrini pozitivni?
- Kakšno bi bilo polje, če bi bili obe elektrini negativni?
- Kam bi morali postaviti elektrino Q3=2 m C, da bo sila nanj enaka nič?
- Koliko bi morala biti elektrina Q3, če jo postavimo med elektrini Q1 in Q2, da bo sila nanjo enaka 0?
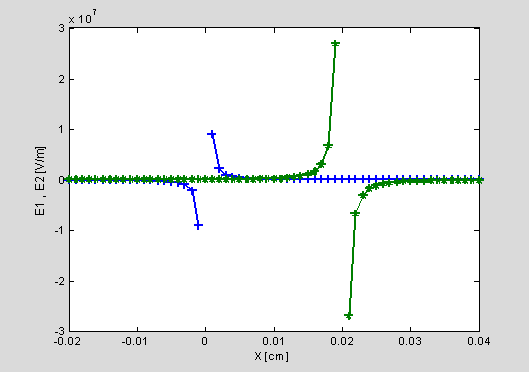
Naloga 2.4: Določite in izrišite električno poljsko jakost vzdolž osi x (y=0,z=0) od x=-3cm do x=3cm s korakom dx=0.5cm za elektrine iz naloge 2.1!
Namen: Seznanitev z izračunom polja za poljubno postavljene elektrine ter seznanitev s problematiko vizualizacije polja.
MLAB: Zapišemo vektor X, ki vsebuje koordinate, kjer želimo računati polje in celotnega v matriko P:
Q1=2e-12;
Q2=-2e-12;
e0=8.854e-12;
k=1/(4*pi*e0);
r1=[1, 1, 1]*1e-2;
r2=[-2,-1,3]*1e-2;
X=[-3:0.1:3]*1e-2;
len=length(X);
Y=zeros(1,len);
Z=Y;
P=[X' Y' Z']; %tvorimo matriko s koordinatami tock P(x,y,z)
P(1,:); % tako zapišemo prvi vektor
for i=1:len
RP1(i,:)=(P(i,:)-r1);
ERP1(i,:)=k*Q1*RP1(i,:)/abs(RP1(i,:)*RP1(i,:)')^3;
RP2(i,:)=(P(i,:)-r2);
ERP2(i,:)=k*Q2*RP2(i,:)/abs(RP2(i,:)*RP2(i,:)')^3;
end
ERP1(:,1); % x komponenta polja, ki ga povzroca elektrina Q2
ERP2(:,1); % x komponenta polja, ki ga povzroca elektrina Q2
E=ERP1 + ERP2;
for i=1:len
Eabs(i)=sqrt(E(i,1)^2+E(i,2)^2+E(i,3)^2);
end
Eabs;
subplot(2,1,1),plot(X,E(:,3),'Linewidth',2)
grid on;
xlabel(' x [m]');
ylabel('Ex [V/m]');
subplot(2,1,2),plot(X,Eabs,'Linewidth',2)
grid on;
xlabel(' x [m]');
ylabel('Abs(E) [V/m]');
Vprašanja:
- Poskušajte si predstavljati, kako bi se spreminjala Ez po x osi? Skicirajte in potem preverite tako, da namesto plota E(:,1) uporabite E(:,3)!
- Kako bi se spreminjal Ez, če bi bila elektrina Q2 na mestu P2(-2,-1,1)?
- Ker je prostorska predstavitev vektorskega polja v treh dimenzijah težka, poskusite skicirati električno poljsko jakost če gledamo le dve dimenziji. Naj bosta točki P1(1,0,1) in P2(-1,0,-1). V tem primeru ležita točki le v (x,z) ravnini, torej je tudi električna poljska jakot v smeri y enaka nič. Kako se sedaj spreminja polje Ez in Ex po oseh x in z?
- Kakšno bi bilo polje Ez(x,y=z=0), Če bi bila elektrina Q1=10 pC?
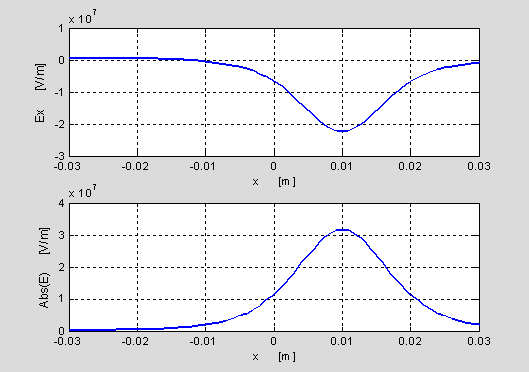
Naloga 2.5: Izrišite 3D graf električne poljske jakosti za elektrino Q1=5 pC postavljeno na mestu P1(1,2)cm. Izrišite polje v območju (0,0) do (4,4)cm!
Namen: Seznanitev s 3D vizualizacijo polja.
MLAB: Točke v prosturu zapišemo v matriko ([X,Y]=meshgrid(0:dx:maxx,0:dy:maxy);). S pomočjo dveh FOR zank precešemo vse tocke in izračunamo polje. Za vizualizacijo uporabimo funkcijo MESH.
Q1=5e-12;
e0=8.854e-12;
k=1/(4*pi*e0);
r1=[1, 2]*1e-2;
dx=0.5e-3;dy=0.5e-3; maxx=4e-2;maxy=4e-2;
x=0:dx:maxx; y=0:dy:maxy;
[X,Y]=meshgrid(0:dx:maxx,0:dy:maxy);
for i=1:1:length(x)
for j=1:1:length(y)
p1x=r1(1,1)-x(i);
p1y=r1(1,2)-y(j);
psqr=sqrt(p1x^2+p1y^2);
if psqr==0
psqr=1e-10;
end
E1x(i,j)=k*Q1*p1x/psqr^3;
E1y(i,j)=k*Q1*p1y/psqr^3;
end
end
Eabs=(sqrt(E1x.^2+E1y.^2));
Emax=max(max(Eabs));
[i,j]=find(Eabs==0);
Eabs(i,j)=Emax;
figure,mesh(X,Y,Eabs)
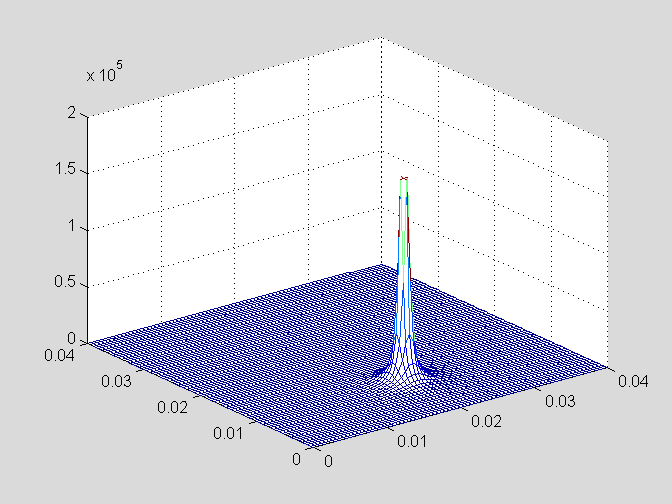
Naloga 2.6: Izrišite 3D graf in konture električne poljske jakosti za elektrine Q1=5 pC, Q2=-2 pC in Q3=-3 pC, ki se nahajajo v točkah P1(1,2) cm, P2 (2,3) cm in P3(1,1). Izrišite konture polja na x-y ravnini v območju (0,0) do (3,3)cm!
Namen: 3D vizualizacija polja, delo s FOR zankami in poljubnim številom elektrin.
MLAB: Podobno kot v prejšnjem primeru, le da imamo več elektrin. Za izris kontur električne poljske jakosti glej (help contourf). Ker se polje spreminja s kvadratom, je za boljšo vizualizacijo koristno izrisati konture (desetiškega) logaritma polja. Poleg tega lahko grafu dodate vektorje, ki kažejo v smeri polja. Najprej je potrebno uporabiti ukaz gradient, ki numerično izračuna odvod vektorja v vseh točkah ter za izris ukaz quiver.
clear all
Q=[5e-12,-2e-12,-3e-12];
e0=8.854e-12;
k=1/(4*pi*e0);
R=1e-2*[1, 2;2,2;1,1];
dx=0.5e-3;dy=0.5e-3; maxx=4e-2;maxy=4e-2;
x=0:dx:maxx; y=0:dy:maxy;
[X,Y]=meshgrid(0:dx:maxx,0:dy:maxy);
N=length(Q);
E1x=zeros(length(x),length(x));
E1y=E1x;
for i=1:1:length(x)
for j=1:1:length(y)
for k=1:1:N
p1x=R(k,1)-x(i);
p1y=R(k,2)-y(j);
psqr=sqrt(p1x^2+p1y^2);
%if psqr==0
% psqr=1e-4;
%end
E1x(i,j)=E1x(i,j)+k*Q(k)*p1x/psqr^3;
E1y(i,j)=E1y(i,j)+k*Q(k)*p1y/psqr^3;
end
end
end
Eabs=(sqrt(E1x.^2+E1y.^2));
Emax=max(max(Eabs));
[i,j]=find(Eabs==0);
%Eabs(i,j)=Emax;
figure,surf(X,Y,log10(Eabs)),colormap hot
figure,[C,h]=contourf(X,Y,log10(Eabs)); colorbar
[U,V]=gradient(log10(Eabs),x,y);
hold on;
quiver(x,y,U,V)
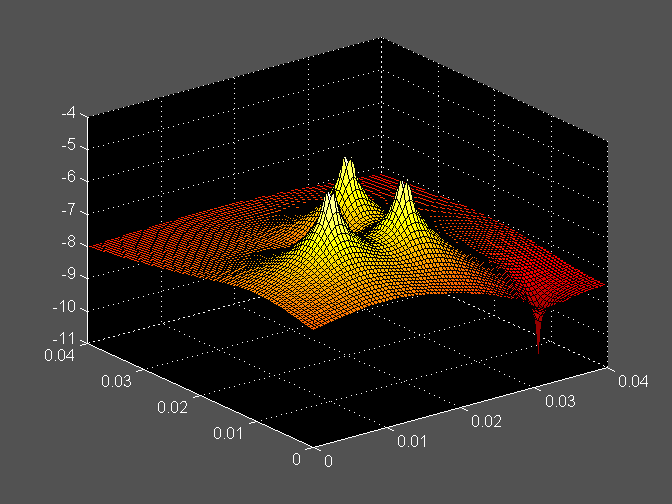
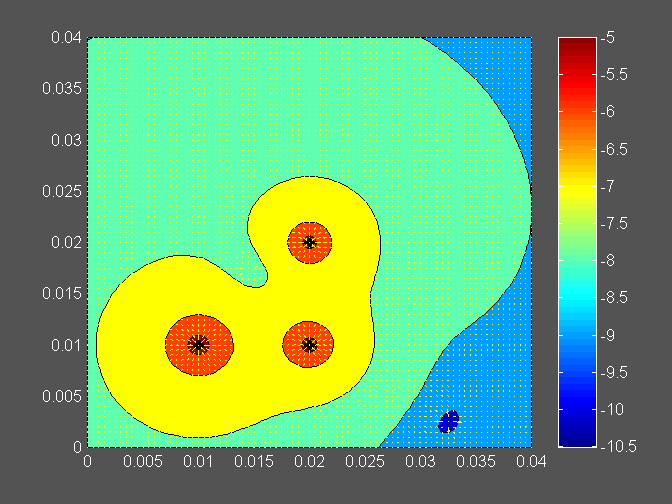Vprašanja:
- Analiziraj polje v primeru dveh enako velikih elektrin!
- Analiziraj polje v primeru dveh enako velikih elektrin nasprotnega predznaka!
- Analiziraj polje v primeru dveh različno velikih elektrin nasprotnega predznaka!
- Analiziraj polje v primeru dveh različno velikih elektrin nasprotnega predznaka!
- Kaj ne vidimo pri konturnem prikazu polja?
- Kakšno je polje v sredini med elektrinama v primerih a) do d)?
- Kakšno je polje daleč stran (v okolici) sistema elektrin za primere a) do d)?
Potencial definiramo kot delo, ki ga opravi elektrostatično polje pri premiku pozitivne elektrine 1As po poljubni poti od neke splošne točke T v prostoru (kjer potencial iščemo), do točkeT0, kjer je potencial enak nič.
Naloga 3.1: Izračunajte in izrišite polje in potencial med koncentričnima prevodnima valjema (koaksialni kabel) z notranjim polmerom rn=1 mm in zunanjim polmerom rz=3mm, če je med njima priključena napetost 25V.
Namen: Izračun potenciala in polja za koaksialni kabel in grafični prikaz.
MLAB: Uporabite ukaz plotyy za izris obeh funkcij na enem plotu.
e0=8.854e-12;
k=1/(4*pi*e0);
U=25; rn=1e-3; rz=3e-3;
q=U*2*pi*e0/(log(rz/rn));
R=0:1e-4:rz;
E=zeros(length(R),1);
V=E;
E=q/(2*pi*e0)./R;
V=q/(2*pi*e0)*log(rz./R);
for i=1:1:length(R)
if R(i)<rn
V(i)=U;
E(i)=0;
end
end
%plot(R,V); xlabel(' Radij [m]'); ylabel(' Potencial [V]');
%figure; plot(R,E); xlabel(' Radij [m]'); ylabel(' El. poljska jakost [V/m]');
% IZRIS POLJA IN POTENCIALA NA ISTI SLIKI Z DVEMA OSEMA
[ax ax1 ax2]=plotyy(R,V,R,E,'plot');
axes(ax(1)); ylabel(' Potencial [V]');
axes(ax(2)); ylabel(' El. poljska jakost [V/m]');
set(ax1,'LineStyle',':')
set(ax1,'Linewidth',3)
set(ax2,'Linewidth',2)
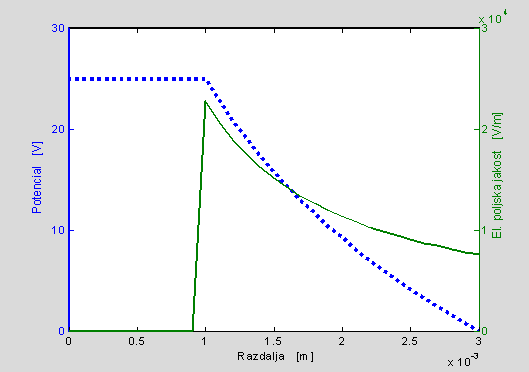
· Vprašanja:
- Kolikšna je največja in koliko najmanjša el. poljska jakost znotraj kabla (med valjema)?
- Kolikšno je polje v okolici kabla?
- V kakšnem razmerju je maksimalna el. poljska jakost za dva koncentrična prevodna valja in dve ravnini, če je med prevodnima ploskvama obeh elementov enaka napetost? Zakaj je tako?
- V kakšnem razmerju sta napetosti, če je med elementoma enako maksimalno polje? Zakaj je ena napetost višja?
- Izrišite ekvipotencialne ploskve in silnice električnega polja! Pomoč: krog izrišeš kot plot(sin(x),cos(x)), kjer gre x od 0 do 2*pi. Uporabi še axis equal.
- Kolikšen sme biti najmanjši in največji polmer notranjega valja, da ne pride do preboja pri prebojni trdnosti zraka 2,1kV/mm? Pomoč: dobimo transcendentno enačbo, ki jo lahko rešimo tabelarično, grafično ali numerično.
- Kolikšna je ploskovna gostota na manjšem in na večjem valju?
Naloga 3.2: Za iste vrednosti radijev in napetosti kot pri nalogi 2.8 le tokrat za primer krogelnega kondenzatorja izračunajte in določite polje in potencial ter odgovorite na vprašanja! Dodatno: na grafu prikažite polje in potencial za ravni (ploščni), cilindrični in krogeljni kondenzator!
Naloga 3.3: Določite el. poljsko jakost in potencial vzdolž naelektrenega obroča radija r=2cm, na katerem je enakomerno razporejena elektrina Q=12nC!
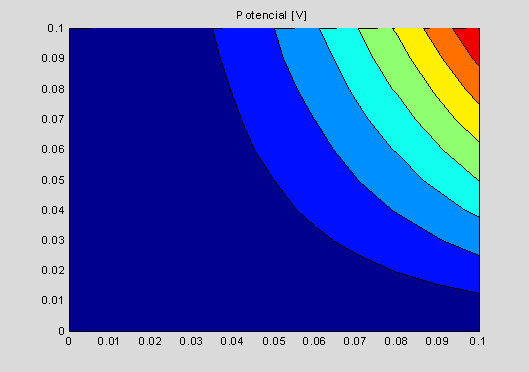
Naloga 3.4: Za elektrine iz naloge 2.6 izračunajte potencial v prostoru ter izrišite ekvipotencialne ploskve in v obliki 3D grafa!
Namen: Izračun potenciala za točkaste elektrine. 2D in 3D vizualizacija potenciala. Komentiranje ekvipotencialnih ploskev dveh enako velikih enako (predznačenih) elektrin.
MLAB: Uporaba funkcije contourf!
Q=[5e-12,-3e-12,-2e-12];
e0=8.854e-12;
k=1/(4*pi*e0);
R=1e-2*[1, 2;2,2;1,1];
dx=0.5e-3;dy=0.5e-3; maxx=4e-2;maxy=4e-2;
x=0:dx:maxx; y=0:dy:maxy;
[X,Y]=meshgrid(0:dx:maxx,0:dy:maxy);
N=length(Q);
V=zeros(length(x),length(y));
for i=1:1:length(x)
for j=1:1:length(y)
for m=1:1:N
p1x=R(m,1)-x(i);
p1y=R(m,2)-y(j);
psqr=sqrt(p1x^2+p1y^2);
V(i,j)=V(i,j)+k*Q(m)/psqr;
end
end
end
%figure,surf(X,Y,V),colormap hot, xlabel(' X os [m]'); ;zlabel('Potencial [V]');
figure,[C,h]=contourf(X,Y,V); colorbar
xlabel(' X os [m]'); ylabel('Y os [m]'); title('Potencial [V]')
Vprašanja:
- V kateri točki je potencial enak nič?
- Kje je potencial pozitiven in kje negativen?
- Izriši ekvipotencialne ploskve za dve enako veliki elektrini istega (nasprotnega) predznaka! Komentiraj!
- Izriši ekvipotencialne ploskve za dve različno veliki elektrini istega (nasprotnega) predznaka! Komentiraj!
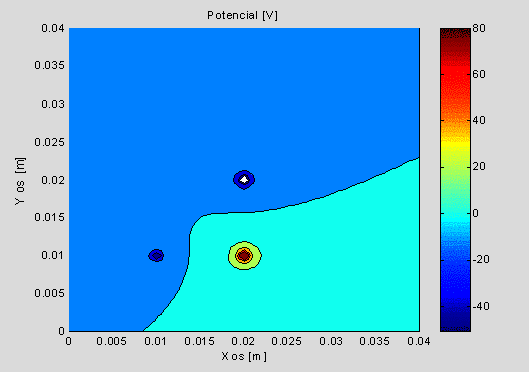
Naloga 3.5: Določi potencial znotraj in zunaj naelektrene krogle z enakomerno porazdeljeno volumsko gostoto elektrin, če je radij krogle 2 cm, spečificna gostota volumsko porazdeljene elektrine pa r =1e-10 C.m-3.
Namen: Uporabite Gaussov stavek za izračun polja in z integracijo polja izračunajte potencial.
Vprašanja:
- Kolikšna napetost je znotraj naelektrene krogle?
- Kolikšna napetost je med med površino krogle in neskončnostjo?
- Kolikšna bi morala biti velikost točkaste elektrine, da bi bil potek polja in potenciala enak za radije večje od radija krogle?
- Pri kateri napetosti in kakšni specifični gostoti enakomerno porazdeljene gostote elektrin med plaščem krogle in notranjostjo bo največja poljska jakost enaka 30kV/cm? Kje bo polje največje?
- Kako se bi polje spremenilo, če
bi se gostota elektrin linearno povečevala z radijem kot
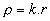
, pri čemer določite konstanto k tako, da bo celotna elektrina enaka, kot v primeru enakomerno porazdeljene elektrine?
Naloga 3.6: Prikaži na grafu potek potencialov podanih v obliki funkcij:
a) V(x,y)=400x2y x [0:10] cm; y[0:10] cm
b) V(x,y)=400xy+ 200*sin(x) x [0:10] cm; y[0:10] cm
c) V(x,y)=200*sin(x)*cos(y) x [0:2] cm; y[0:2] cm
Iz grafov poskusite skicirati konture električne poljske jakosti! Numerično in analitično določite in izrišite električno poljsko jakost za vse tri primere.
Namen: Izračun in prikaz polja iz znane porazdelitve potenciala.
Pozor: Ne izrisite polja z računalnikom, predno ga ne poskusite skicirati sami! Kjer se potencial najhitreje spreminja je polje največje.
MLAB: Točke v x,y ravnini določite z ukazom meshgrid (naloga 2.5), pri določitvi funkcije pa pazite na to, da dosežemo množenje posameznih elementov matrike z ukazom (.*). Za prikaz potenciala uporabite ukaz contourf ali surf. Numerično odvajanje dosežemo z uporabo funkcije gradient ([Ex,Ey]=gradient(V,dx,dy)), kjer st dx in dy korak med točkami v x in y smeri.
dx=xmax/10;
[X,Y]=meshgrid(0:dx:xmax,0:dx:xmax);
V=400.*(X.^2).*Y;
%V=200*sin(X).*cos(Y);
contourf(X,Y,V);
title('Potencial [V]')
%surf(X,Y,V)
[Ex,Ey]=gradient(-V,dx,dx);
Eabs=sqrt(Ex.^2+Ey.^2);
%figure, surf(X,Y,Eabs)
Naloga 4.1P: Primer uporabe elektrostatičnega polja: Določitev prebojne napetosti koaksialnega kabla.
Če uporabimo koaksialni kabel za prenos električne moči, je polmer kabla določen s tokom, ki teče skozi kabel ter ostale dimenzije z izolacijskim materialom in napetostjo. Predpostavimo notranji radij rn=0,4 cm, ki je obdan z dielektrikom iz gume (e rg=3,2) in poliestra (e rp=2,6). Dimenzionirajte koaksialni kabel tako, da bo delal pri napetosti 20 kV. Da bi preprečili preboj v dielektrikih (pri udaru strele in drugih zunanjih pogojih), ne sme maksimalno polje znotraj dielektrika preseči 25% maksimalne prebojne trdnosti, ki je 25.106 V/m za gumo in 20.106 V/m za poliester! Med zunanjim in notranjim plaščem naj napetost ne bo večja od 20 kV.
Postopek: Zapišemo enačbi za maksimalno prebojno trdnost in določimo radij zunanje plasti notranjega dielektrika ter elektrino, ki se nabere na žili. Napišemo enačbo za napetost kot integral polja od notranjega do zunanjega radija in iz enačbe določimo še zunanji radij.
Dodatno: Izrišite krivuje poteka električne poljske jakosti, pri zagotovljenem pogoju za preboj, če spreminjamo notranji radij od 1 do 5 mm. Če bi želeli povečati delovno napetost od 20
na 30 kV, kakšna dielektrika bi morali uporabiti, če bi dimenzije kabla obdržali iste? Kakšen postopek bi potrebovali, če bi namesto notranjega radija imeli željen zunanji radij in bi iskali primeren notranji radij?
6. Energija elektrostatičnega polja
Za točkaste elektrine izračunamo energijo iz znanih vrednosti električnega potenciala na mestu elektrine in velikosti elektrin.
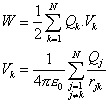
V primeru porazdeljenih elektrin pa velja izraz
.
Naloga 5.1: Za porazdelitev elektrin iz naloge 1.2 določite elektrostatično energijo.
Vprašanja:
- Kaj pomeni dobljena številka? Kako jo lahko interpretirate?
- Kolikšno delo moramo opraviti, da premaknemo elektrino Q3 v koordinatno izhodišče?
- Kakšna je razlika med pozitivnim in negativnim predznakom, ki ga dobimo pri premikanju elektrin?
- Kolišna je energija sistema, če postavimo na mesto P4(3,3)cm še dodatno energijo Q4=2 pC?
A. Biran, M. Breiner: "Matlab 5 for engineers", Addison-Wesley Publishing Company, 1995.
D. Hanselman, B. Littlefield: "Mastering MATLAB :
a comprehensive tutorial and reference",
D.J. Higham, N.J. Higham: "MATLAB guide",
W. J. Palm : "Introduction to MATLAB 6 for engineers", McGraw-Hill, 2001.
Povezave na internetu: (opozorilo: povezave na internetne strani se s časom lahko spremenijo)
Matlab Basics Tutorial (Carnegie Mellon), http://www.engin.umich.edu/group/ctm/basic/basic.html
Matlab Tutorial Information (Hosted by the UNH Dept. of Mathematics and Statistics Kingsbury Hall University of New Hampshire), http://www.cyclismo.org/tutorial/matlab/
Matlab tutorial (Kermit Sigmon, University of Florida, 1993), http://www.mines.utah.edu/gg_computer_seminar/matlab/matlab.html
Matlab Summary and Tutorial (
Matlab tutorial (Mathworks inc.), http://www.mathworks.com/academia/student_center/tutorials/
Povezave na druge strani iz strani:
MATLAB Educational Sites (University
Osnovna stran programa Matlab: http://www.mathworks.com/