OSNOVE ELEKTROTEHNIKE s programom MATLAB
1. Coulombov zakon
Sila med elektrinama je usmerjena vzdolž premice na kateri se nahajata elektrini. Spreminja se inverzno proporcionalno s kvadratom razdalje med elektrinama in je proporcionalna velikosti obeh e
lektrin:![]()
\* MERGEFORMAT (.)01
kjer je ![]() enotin vektor v smeri od elektrine Q1 do Q2. Če je elektrin več, je sila na elektrino (vektorska) vsota prispevkov posameznih elektrin (superpozicija!).
enotin vektor v smeri od elektrine Q1 do Q2. Če je elektrin več, je sila na elektrino (vektorska) vsota prispevkov posameznih elektrin (superpozicija!).
Naloga 1.1: Elektrina Q1=200 m C se nahaja v središču koordinatnega sistema P(0,0,0)m. S kolikšno silo deluje na elektrino Q2=-300 m C, ki se nahaja v točki P2(1,3,4) cm?
Q2=-30e-6 % če vrstice ne zaključimo z znakom";", se izpiše rezultat
e0=8.854e-12; % dielektričnost vakuuma
k=1/(4*pi*e0);
Q2 =-3.0000e-005
r1=[0, 0, 0]; %vrstični vektorr2=[1,3,2]*1e-2;
r21=r2-r1;
% vektor, ki kaže od vektorja r1 proti vektorju r2Abs_r21=sqrt(r21*r21'); % absolutna vrednost vektorja r21 dobimo z množenjem vektorja r21 s transponiranim vektorjem r21'
er21=r21/Abs_r21 % normalni vektorj v smeri r21 er21 =
0.2673 0.8018 0.5345
3.8519e+003
F21 =1.0e+003 *
-1.0295 -3.0884 -2.0589
Vprašanja:
a) V katero smer kaže sila na elektrino?
b) V kateri smeri je največja sila?
c) Koliko je absolutna vrednost sile (enote!)?
d) Koliko prostih elektronov vsebujeta Q1 in O2?
Naloga 1.2: Poleg dveh elektrin iz naloge 1 imamo še elektrino Q3=100 m C na mestu P3(-1,0,2)cm. Vsota vseh treh elektrin je enaka 0, kar zaključuje sistem elektrin. Ponovno izračunajte silo na elektrino Q2!
Ker smo silo Q1 na Q2 že izračunali, izračunamo le še prispevek elektrine Q3 in prispevka seštejemo:
Q3=100e-6;r3=[-1,0,2]*1e-2;
r23=r2-r3
Abs_r23=sqrt(r23*r23');
er23=r23/Abs_r23;
F23=k*Q1*Q2*er23/Abs_r23^2 % sila na elektrino Q2
Abs_F23=sqrt(F23*F23')
F2=F21+F23 % celotna sila na elektrino Q2
r23 =
0.0200 0.0300 0
F23 =
1.0e+003 *
-2.3010 -3.4515 0
Abs_F23 =
4.1482e+003
F2 =
1.0e+003 *
-3.3305 -6.5399 -2.0589
Vprašanja:
Naloga 1.3 Določite silo na elektrino Q1 iz naloge 1.1!
Naloga 1.4 Določite silo na elektrino Q1 iz naloge 1.2!
Naloga 1.5 Elektrinam v nalogi 1.2 poljubno spreminjamo predznak. Kdaj bo sila na elektrino Q3 največja in kdaj najmanjša in koliko bo?
2. Električno polje
Električno poljsko jakost definiramo kot silo na enoto
poskusne elektrine q:![]() . V tem smislu lahko izračunamo električno poljsko jakost povsod v prostoru, kjer se nahajajo elektrine. V prostoru N točkastih elektrin je električna poljska jakost na mestu določenim z vektorjem ri vsota prispevkov vseh elektrin:
. V tem smislu lahko izračunamo električno poljsko jakost povsod v prostoru, kjer se nahajajo elektrine. V prostoru N točkastih elektrin je električna poljska jakost na mestu določenim z vektorjem ri vsota prispevkov vseh elektrin:
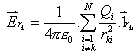
Naloga 2.1 V prostoru imamo elektrini Q1=2 pC v točki P1(1,1,1)mm in Q2=-2 pC v točki P2(-2,-1,3) cm. Koliko je električna poljska jakost v središču koordinatnega sistema?
Q1=2e-12;
Q2=-2e-12;
e0=8.854e-12;
r0=[0,0,0];
r1=[1, 1, 1]*1e-2;
r2=[-2,-1,3]*1e-2;
% tvorimo vektor, ki kaže od točke P2 (vektor r2) proti točki središču k.s. (vektor r0)
r20=r0-r2;
r10=r1-r0;
Abs_r20=sqrt(r20*r20');
er20=r20/Abs_r20;
Abs_r10=sqrt(r10*r10');
er10=r10/Abs_r10;
E20=k*Q2*er20/Abs_r20^2 % polje zaradi elektrine Q2
E10=k*Q1*er10/Abs_r10^2 % polje zaradi elektrine Q1
E0=E20+E10
Abs_E0=sqrt(E0*E0')
E20 =
6.8631 3.4315 -10.2946
E10 =
34.5938 34.5938 34.5938
E0 =
41.4569 38.0254 24.2992
Abs_E0 =
61.2785
Naloga 2.2: Določite električno poljsko jakost na mestu P4(1,1,1)cm za elektrine iz naloge 1.2!
Naloga 2.3: Elektrini Q1=1 C in Q2=-3 m C sta razmaknjeni za 12 cm in se nahajata vzdolž x osi. Izriši električno poljsko jakost vzdolž x osi!
clear allQ1=1e-6;
Q2=-3e-6;
e0=8.854e-12;
k=1/(4*pi*e0);
X=(-5:0.5:20)*1e-2; % koordinate x osi
% Q1 postavimo v koord. izhodišce, Q2 pa 12 cm stran v smeri poz. x osi
 E1=k*Q1*X./X.^3; % operator za deljenje vektorja je "./"
E1=k*Q1*X./X.^3; % operator za deljenje vektorja je "./"
XT=12*1e-2*ones(1,length(X)); %vektor z vrednostmi pozicije lektrine Q2
Xraz=X-XT;
E2=k*Q2*Xraz./Xraz.^3;
E=E1+E2;
plot(X,E1,X,E2,X,E,'o')
xlabel('X os [cm]');
ylabel('E1, E2 in E1+E2 [V/m]');
% Če želimo izpisati točno lego:
a=find(E<0);
x=int2str(1e3*X(a(1)));
answer=['Polje je nic pri X='x ' mm!'];
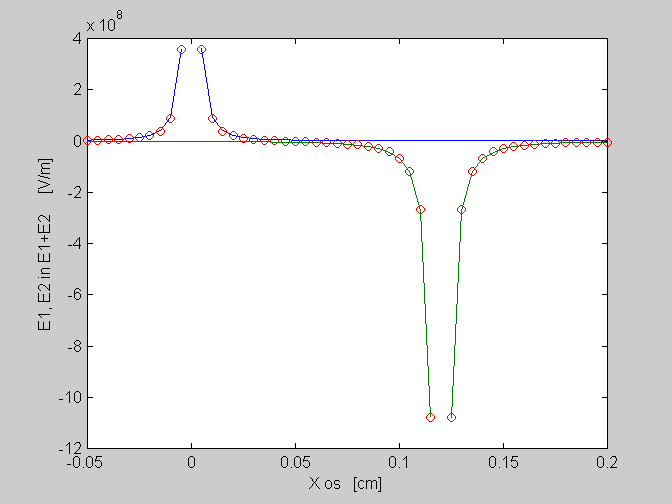
Naloga 2.4: Določite in izrišite električno poljsko jakost vzdolž osi x (y=0,z=0) od x=-3cm do x=3cm s korakom dx=0.5cm za elektrine iz naloge 2.1!
Zapišemo vektor X, ki vsebuje koordinate, kjer želimo računati polje in celotnega v matriko P:
clear allQ1=2e-12;
Q2=-2e-12;
e0=8.854e-12;
k=1/(4*pi*e0);
r1=[1, 1, 1]*1e-2;
r2=[-2,-1,3]*1e-2;
X=[-3:0.1:3]*1e-2;
len=length(X);
Y=zeros(1,len);
Z=Y;
P=[X' Y' Z']; %tvorimo matriko s koordinatami tock P(x,y,z)
P(1,:); % tako zapišemo prvi vektor
for i=1:len
RP1(i,:)=(P(i,:)-r1);
ERP1(i,:)=k*Q1*RP1(i,:)/(RP1(i,:)*RP1(i,:)')^3;
RP2(i,:)=(P(i,:)-r2);
ERP2(i,:)=k*Q2*RP2(i,:)/(RP2(i,:)*RP2(i,:)')^3;
end
ERP1(:,1); % x komponenta polja, ki ga povzroča elektrina Q2
ERP2(:,1); % x komponenta polja, ki ga povzroča elektrina Q2
E=ERP1 + ERP2;
for i=1:len
Eabs(i)=sqrt(E(i,1)^2+E(i,2)^2+E(i,3)^2);
end
Eabs;
subplot(2,1,1),plot(X,E(:,3))
grid on;
xlabel(' x [m]');
ylabel('Ex [V/m]');
subplot(2,1,2),plot(X,Eabs)
grid on;
xlabel(' x [m]');
ylabel('AbsE [V/m]');
Vprašanja:
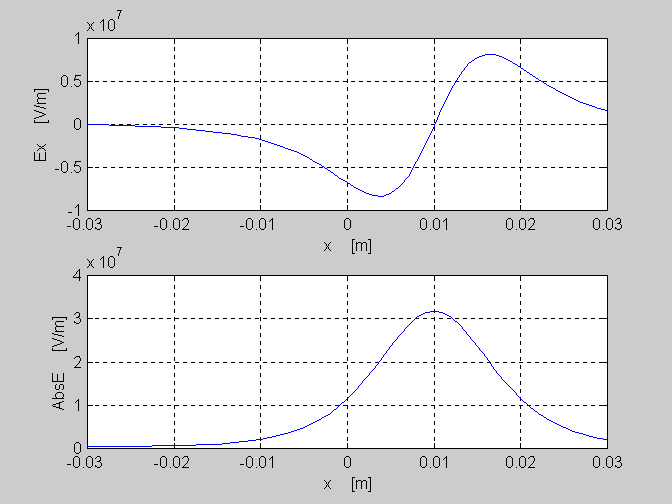
Naloga 2.5: Izrišite 3D graf električne poljske jakosti za elektrino Q1=5e-12 C postavljeno na mestu P1(1,2)cm. Izrišite polje v območju (0,0) do (4,4)cm!
clear all
Q1=5e-12;
e0=8.854e-12;
k=1/(4*pi*e0);
r1=[1, 2]*1e-2;
dx=0.5e-3;dy=0.5e-3; maxx=4e-2;maxy=4e-2;
x=0:dx:maxx; y=0:dy:maxy;
 [X,Y]=meshgrid(0:dx:maxx,0:dy:maxy);
[X,Y]=meshgrid(0:dx:maxx,0:dy:maxy);
for i=1:1:length(x)
for j=1:1:length(y)
p1x=r1(1,1)-x(i);
p1y=r1(1,2)-y(j);
psqr=sqrt(p1x^2+p1y^2);
if psqr==0
psqr=1e-10;
end
E1x(i,j)=k*Q1*p1x/psqr^3;
E1y(i,j)=k*Q1*p1y/psqr^3;
end
end
Eabs=(sqrt(E1x.^2+E1y.^2));
Emax=max(max(Eabs));
[i,j]=find(Eabs==0);
Eabs(i,j)=Emax;
figure,mesh(Eabs)
Naloga 2.6: Izriši 3D graf in konture električne poljske jakosti za elektrine Q1=5e-12 C, Q2=-2e-12 C in Q3=-3e-12C, na mestu P1(1,2) cm, P2 (2,3) cm in P3(1,1). Izriši konture polja na x-y ravnini v območju (0,0) do (3,3)cm!
clear allQ=[5e-12,-2e-12,-3e-12];
e0=8.854e-12;
k=1/(4*pi*e0);
R=1e-2*[1, 2;2,2;1,1];
% KORAK VZDOLZ X IN Y OSI TER MAX X IN Y
dx=0.5e-3;dy=0.5e-3; maxx=3e-2;maxy=3e-2;
x=0:dx:maxx; y=0:dy:maxy;
¸% MREŽA NA X-Y RAVNINI, KJER BOMO IZRISALI POLJE
[X,Y]=meshgrid(0:dx:maxx,0:dy:maxy);
N=length(Q);
%
MATRIKA VREDNOSTI POLJA JE V ZAČETKU PRAZNA (ENAKA NIČ)E1x=zeros(length(x),length(x));
E1y=E1x;
% ZA VSAKO TOČKO V MREŽI DOLOČIMO X IN Y KOMPONENTO POLJA
for i=1:1:length(x)
for j=1:1:length(y)
for k=1:1:N
p1x=R(k,1)-x(i);
p1y=R(k,2)-y(j);
psqr=sqrt(p1x.^2+p1y.^2);
%if psqr==0
% psqr=1e-4;
%end
E1x(i,j)=E1x(i,j)+k*Q(k)*p1x/psqr^3;
E1y(i,j)=E1y(i,j)+k*Q(k)*p1y/psqr^3;
end
end
end
% DOLOČIMO MATRIKO ABSOLUTNIH VREDNOSTI POLJA IN POIŠČEMO MAX POLJE
Eabs=(sqrt(E1x.^2+E1y.^2));
Emax=max(max(Eabs));
%figure,surf((E1x)),colormap hot
figure,contourf(X,Y,Eabs), colorbar
Naloga 2.7: Določite električno poljsko jakost dipola ![]() ter rezultat primerjajte z analitičnim vzdolž osi dipola!
ter rezultat primerjajte z analitičnim vzdolž osi dipola!
Naloga 2.8: Izračunajte in izrišite polje in potencial med koncentričnima prevodnima valjema (koaksialni kabel) z notranjim polmerom rn=1 mm in zunanjim polmerom rz=3mm, če je med njima priključena napetost 25V.
Vprašanja:
Naloga 2.9: Za iste vrednsti radijev in napetosti le tokrat v primeru krogelnega kondenzatorja izračunaj in določi polje in potencial ter odgovori na vprašanja! Dodatno: na grafu prikaži polje in potencial za ravni (ploščni), cilindrični in krogeljni kondenzator!